Since the polynomial has a factor of x+8, synthetic division of the given polynomial by −8 may be completed. Recall the factor is in the form, (x-a); equals , so a=-8. Synthetic division reveals x^3+7x^2-20x-96=(x+8)(x^2-x-12).The factor x^2-x-12, which can be further factored as (x+3)(x-4). Setting each factor equal to zero gives x=-3 and x=4. Thus, two more zeros of the polynomial are x=-3 and x=4. The zero that may be directly determined from the problem is x=-8.
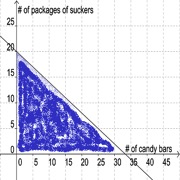
The y-intercept of the inequality is 20, and the slope is −0.6. The slope can be determined by calculating the ratio of the change in y-values per change in corresponding x-values. Using the y-intercept and the point, (25, 5), the slope can be written as (5-20)/(25-0), which equals −0.6. Since the evaluation of the inequality for x- and y-values at the origin produces a true statement, the side of the plane containing the point, (0, 0) should be shaded. The inequality, 0.75x+1.25y≤25, solved for y, may be written as y≤-0.6x+20.
When completing the square, the coefficient of the x-term, or −6, should be divided by 2 and then squared. Doing so gives 9. This constant should be added to both sides of the equation. Thus, the equation may be written as x^2-6x+9=27. The left side of the equation may be written as 〖(x-3)〗^2. Thus, the equation that may be used to find the solution of the equation, using the method of completing the square, is 〖(x-3)〗^2=27.