SA = 4Πr2 finds the radius.
4(3.14)r2 = 1,476cm2
12.56r2 = 1,476cm2
r2 = 117.51592356687898
r = 10.840476168825749 (or 10.84)
Place the value of the radius in the circumference formula (C = 2Πr)
C = 2(3.14)(10.84) = 68.0752 or approximately 68.1 (Answer 1).
To determine the mean, add all numbers together and divide the sum (143) by the quantity (6).
Take the two middle numbers in numerical order (53 and 82) and add them together. Then, divide by 2.
To determine the median, find the two middle numbers in numeric order (5 and 5) and divide by 2.
In this case, the numeric order is
2, 2, 2, 5, 5, 5, 5 ,5, 10, 10, 10, 10, 10, 10
7 occurs in the highest quantity in the 24-number pair (9 times). This makes it the mode.
If y = 3x - 87, then the following is true per the substitution method:
3x + 2(3x - 87) = 21
3x + 6x - 174 = 21
9x = 195
x = 21.67
y = 3(21.67) - 87
y = -21.99
Let n = the integer.
The product of two values is the result of multiplying them. "Increased by" means to use addition. Therefore, you get this equation:
6n + 13 = -14
Isolate the variable.
6n = -27
Divide both sides by 6.
n = -4.5
Advertisement
Isolate the variable by adding 11 to both sides of the equation right away. You'll be left with:
9c2 = 729
Divide both sides by 9.
Isolate the variable by adding 5 to both sides.
-5x - 5 + 5 > 15 + 5
You're left with this: -5x > 20
Continue the operation, dividing both sides by -5 and reversing the comparison because we are dealing with a negative number.
x < -4
Now plug -4 into the original inequality.
-5(-4) - 5 > 15
20 - 5 > 15
15 > 15
Since 15 is equal to 15 and not greater than, we know that any number below -4 will cause the original inequality (-5x - 5 > 15) to be true; therefore, x > -4, so Answer 1 is correct.
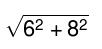
The exponents in the square root must first be evaluated in accordance with the order of operations (PEMDAS: Parentheses, Exponents, Multiplication, Division, Addition, Subtraction), after which the total may be determined and the square root can then be evaluated. The formula is reduced to: 36=64 = 100 = 10.
Regardless of what the signs of the individual points are, keep in mind that distance is always a positive number. Therefore, an absolute value is required in the right response.
Since -1 is halfway between -2 and 0, it must be the starting point. Since it lies in the middle of points 4 and 6, the second point must be 5. To get the right response, divide one point by the other and nest the expression inside an absolute value:
AB = |b − a| or |a − b|
= |−1 − 5|
Decimal numbers can be multiplied together by right-aligning them vertically and multiplying the values as normal while disregarding the decimal points until the product is found. The amount of digits to the right of the decimal points in the values multiplied determines where the decimal point is placed in the product. In this case, there are three digits to the right of the decimal points: 32 and 2, so the product must also have three digits to the right of the decimal: 26624 becomes 26.624 to satisfy this condition.
A building can be painted in 5 days by 10 persons. In 5 days, each person paints a 1/10 of the building. In 5 days, 7 individuals would paint 7 × 1/10 of the building, and 7 people would paint 7/10 of the building.
3.25 feet equals one meter 1 foot = 1÷3.25 meters 21 feet = 21×1÷3.25 = 6.4615 meters
Advertisement
y =15 – 3x and y = 0 15 – 3x = 0 3x = 15 x = 5
The right order is evident if 1/4, 2/3, 4/7, and 1/2 are transformed to fractions with the common denominators 21/84, 56/84, 48/84, and 42/84.
The absolute values |a| or abs(a) can be used to calculate the distance between two numbers. The distance between these numbers is abs(-3/7 − -2/3 ) = abs(-(3/7 -2/3)) = abs(3/7 -2/3) = abs(9/21 – 14/21) = abs(-5/21 ) =5/21
In order for the two shorter sides to meet, the other side must be 5 inches long. The triangle's perimeter is its circumference, which is 5 + 5 + 2 = 12.
This cylinder has a volume of 6283. (pi)r2h = 6283. The height is h. (pi) is 3.14 h = 6283÷(pi)÷100 = 19.999…. h = 20 The cylinder has a 20-inch height.
When h = 0, you reach the platform. You must find the solution to the equation 0 =-t2+3t+10. Rearranging this yields t2-3t-10 = 0. Consequently, (t - 5)(t + 2) = 0. The answer to the equation is t = 5 or -2. It is impossible for t to be -2 since t is a time. The journey of the rocket to the platform lasts 5 seconds.
Click for the next FREE GED Test