GED Mathematical reasoning
If a class has 10 men and 14 women, what is the ratio of men to the class?
The ratio to the class would mean the following: How many men are there in comparison to the class as a whole (men and women combined).
If rope costs $3.20 per yard, or $0.15 per inch, which is the better deal?
NOTE: 1 yard equals 3 feet equals 36 inches
Breaking down the word problem, you're essentially left with two operations: division and multiplication.
Which of the following ratio pairs forms a proportion?
Answer 2 is the only answer in which the two ratios would be the same with a common denominator.
The line connecting points (3,-6) and (-9,2) has slope:
The equation for determining slope is as follows: m=y2 - y1x2 - x1 where x1 is not equal to x2.
>A line with the coordinates (7,y) and (-2,-4) has slope 3/4. What is the value of y?
The equation for determining slope is as follows: m=y2 - y1/x2 - x1 where x1 is not equal to x2.
Solve for b:
a = 14
b = ?
c = 50
Use the equation a2 + b2 = c2, plug in the known values, and solve.
Two supplementary angles have measures of 9x degrees and 3x degrees. What is the measure of the longer angle?
Supplementary angles must add up to 180 degrees. Using that logic, you can solve for x.
Advertisement
Determine the coordinates for the midpoint of a segment with the following endpoints: (12,-8) and (8,-4).
The following can help you determine midpoint coordinates: x1+x2/2, y1+y2/2
A triangle has an area of 110 square inches and a base of 15 inches. Which answer best pinpoints the height?
To determine the area of a triangle, use the equation A=1/2bh (or base times height) The problem gives you the area as being 110 square inches. Plug that in for A. Next, plug in 15 inches for base (also given) and solve for h.
Scott must provide pricing quotes to prospective clients for his house cleaning business. By starting with a $25 base fee and adding $8 for each bathroom and $4 for each additional room, he calculates his price. Which of the following best describes his price quotation formula if he uses P for the price, B for the bathroom, and R for the other rooms?
The total amount of costs will be represented by the price quote, P. Given that a base charge of $25 is assumed, we may start by stating the price quote as P = $25. Our price quote is now P = $25 + $8B, which adds $8 for each bathroom, denoted by the variable B, to the $25 base payment. The next step is to add $4 for every additional room or R, bringing the total price to P = $25 + $8B + $4R.
In the coordinate plane, what are the coordinates of the point?
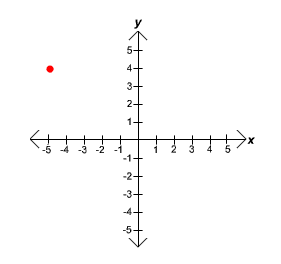
The origin, denoted as (0, 0), where the horizontal x-axis and vertical y-axis intersect, forms the center of the coordinate plane. The coordinate system (x, y) is used to represent points on a plane that have both an x coordinate and a y coordinate. Positive and negative x values are above and below the origin, respectively, whereas negative and positive y values are to the left and right of the origin. In this instance, the point lies above and to the left of the origin. The only response option with a negative x coordinate must be the right one.
Find f(2.5) using the formula f(x) = 2x2 3x + 7.
This is a function issue, where a function connects an input to an output. To find (2.5), replace every x in the original function with 2.5, then evaluate the following expression:
ƒ(2.5) = 2(2.5)2 − 3(2.5) +7
ƒ(2.5) = 2(6.25) − 7.5 + 7
ƒ(2.5) = 12.5 − 7.5 + 7
ƒ(2.5) = 12
Calculate 5x + 8 < 3(x + 2).
After simplifying the expressions using the PEMDAS method, combine like terms before isolating the variable. Equations and inequality can be treated similarly, but there is one key distinction: when multiplying or dividing either side of an inequality by a negative value, the inequality symbol's direction must change.
In this instance, multiply the number three via the parenthesis first before separating the variable:
5x + 8 < 3(x + 2)
5x + 8 < 3x + 6
2x + 8 < 6
2x < −2
x < −1
Simplify (x^6)(x^5)
Recall that the multiplication of terms sharing the same base can be simplified by adding the exponents: x^a * x^b = x^(a + b). If you forget this rule, you can easily derive it by thinking about the straightforward instance of 2^1 * 2^2, which can also be represented as 2 * 2 * 2 or 2^3. Therefore, the phrase in this instance can be summarised as follows:
(x^6) (x^5) = x^5+6
= x^11
Advertisement
The area of the circle shown in the picture is 100π. What is the circle's diameter (D)?

Area = π * r^2
where "r" is the radius of the circle.
In the given information, the area of the circle is 100π. So we have:
100π = π * r^2
Now, let's solve for ""r"":
r^2 = 100
Taking the square root of both sides:
r = √100
r = 10
Now, we know the radius (r) of the circle is 10 units. And the diameter (D) is twice the radius:
D = 2 * r
D = 2 * 10
D = 20
Max first found his math class challenging, but he has been working hard to raise his grades. He is hoping that his final average exam score will be 75 because he has one more test to take. In order to end the year with an average score of 75, what grade must he achieve on Test 6?
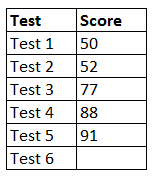
Average = total data points divided by total data points
75 = (50 + 52 + 77 + 88 + 91 + x) ÷ 6
Now calculate x. Begin by adding:
75 = (358 + x) ÷ 6
Next, multiply both sides by 6 to remove the denominator:
450 = 358 + x
The final stage is to take 358 away from each side.
x = 92
If a = −4, and b = 3, what is |a − b|?
The absolute value of the difference is indicated by the vertical bars surrounding a and b. The distance between a simplified expression and 0 is an expression's absolute value, which is always positive. In the expression, replace the given numbers for a and b, calculate the difference, and then add the absolute value to make the expression positive.
|a − b|
= |−4 − 3|
= |−7| = 7
Remember that −4 − 3 is equivalent to −4 + −3 = −7
What is the probability of choosing a man from a group of 4 men and 8 women?
Number of men = 4
Total number of individuals = 4 (men) + 8 (women) = 12
Now, the probability of choosing a man is given by:
Probability = (Number of men) / (Total number of individuals)
Probability = 4 / 12
Now, let's simplify the fraction:
Probability = 1/3
There are 46% female pupils in Kingsport School. How many men attend this high school if there are 1250 students enrolled overall?
If 46% of the total number of students is female, then 100% − 46% = 54% of the students are male. To determine the proportion of male pupils, divide the total by 54 percent.
Recall that 54% is equivalent to 54 ÷ 100, or 0.54:
0.54 * 1250 = 675.
The table displays Erin's earnings and outlays during the first five months of 2012. Which two months did she save the most money?
Calculate the two months with the biggest difference by deducting each expense in the spending column from its corresponding revenue.
January: $3020 − $2370 = $650
February: $2827 − $2012 = $815
March: $3589 − $2620 = $969
April: $3424 − $2630 = $794
May: $3540 − $2570 = $970
Between March and May, Erin saves the most money.